Chapter 12 Quantifying Uncertainty
Chapter 12 Quantifying Uncertainty
Acting Under Uncertainty

- 不論是基於部分觀察性、不決定性 或是兩者結合導致的不確定性 我們都需要想辦法處理
- 以牙醫處理牙痛為例子

- 列舉無窮情況是不可能的

- 轉換成蛀牙導致牙痛 => 但並非所有蛀牙都會牙痛
- 我們需要考慮所有情形+蛀牙 導致牙痛

- 導致失敗的三個原因
- 懶惰、理論無知、實務無知

- 藉由機率幫助我們量化問題
- 為何不是0, 1

- 根據不同的知識狀態 有不同的機率

Uncertainty and rational decisions

- 效用理論 根據效用性來決定agent的偏好

- 決策理論 = 機率理論 + 效用理論
- 一種理性的agent被認為是 行動的平均效益最高 稱之為MEU
What probabilities are about

- 樣本空間
- 樣本空間內機率總合為1 所有機率皆借於0~1之間

- 對於任意命題 命題的機率就是任何滿足該命題的world的機率總和

- 先驗命題 無前提條件

- 有些時候我們會獲得一些證據
- 後驗命題 條件機率

- 例子: 下決定之前 agent要考慮所有觀察到的證據

- 在知道牙痛 且沒有其他證據之下 蛀牙的機率為0.6

- 如何計算條件機率
- product rule
Lang. of propositions in prob. assertions

- a 或 ~a
- 其他例子

- 向量表示 用於簡化書寫

- 使用機率密度函數 來表示連續的 Random variable 的機率
- 簡化表示 在連續隨機變數空間的一點

- 聯合機率分布
- 簡化書寫形式
- 如果指定了一種命題 變成單向量 可以寫回普通機率形式

- 機率模型就是聯合了所有的 random variable
Prob. axioms and their reasonableness
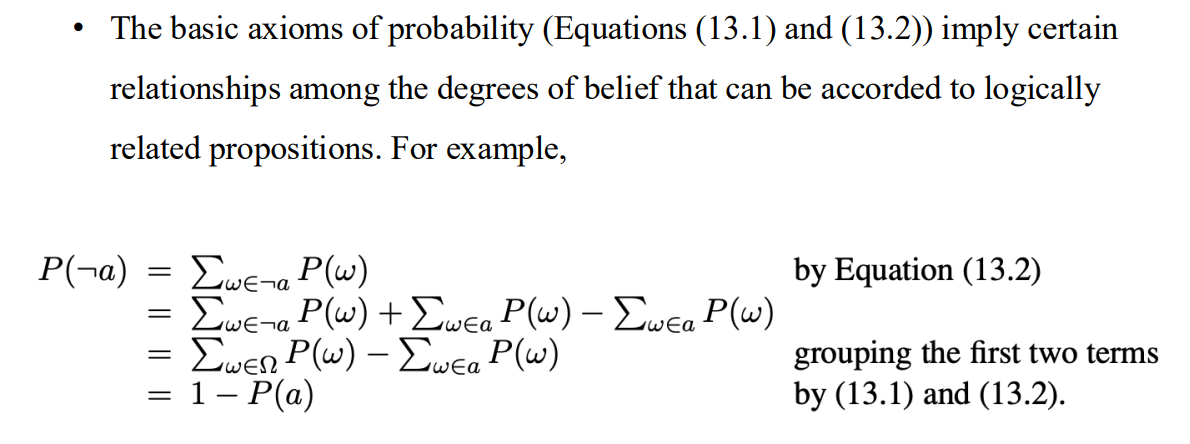
- 1-P(a) = P(~a)

- 連集的計算
Inference Using Full Joint Distributions
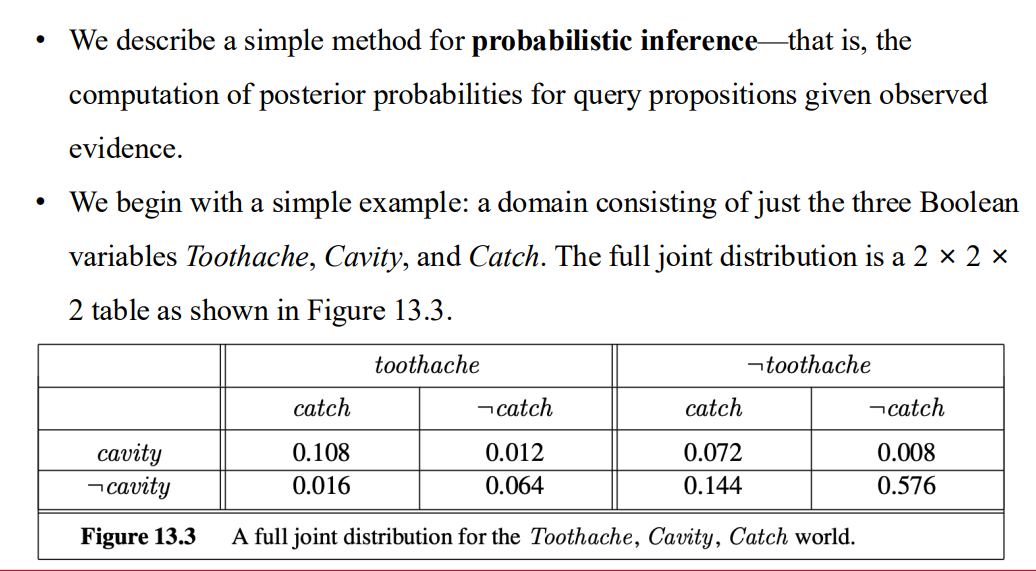

- 根據前面的定理 透過簡單的相加就可以算出來連集

- 邊緣化 或求和 => 將其他變數的影響消去

- 前者的變形 條件化
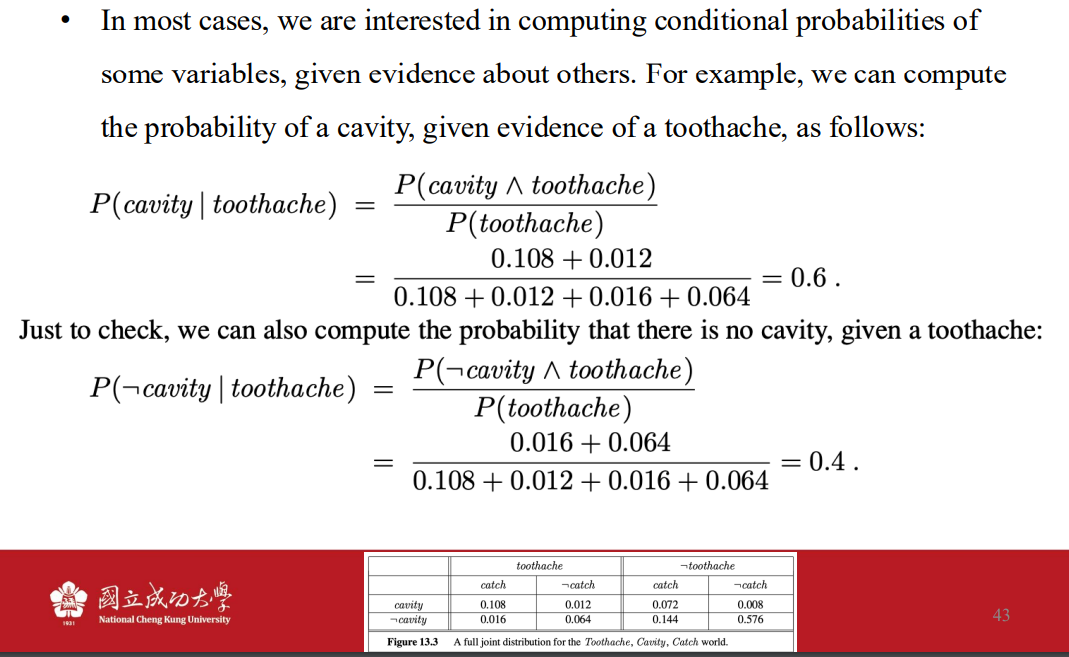
- 一個計算的例子

- 將條件機率的分母寫成常數 => 變成一個函數 用來映射向量
- 因為映射回去 向量各位置上機率的總和變成1 => 該函數的行為相當於標準化
- 因此在不知道函數行為的情況下 我們可以用標準化來計算 更加方便


- 得到以上結論
Independence

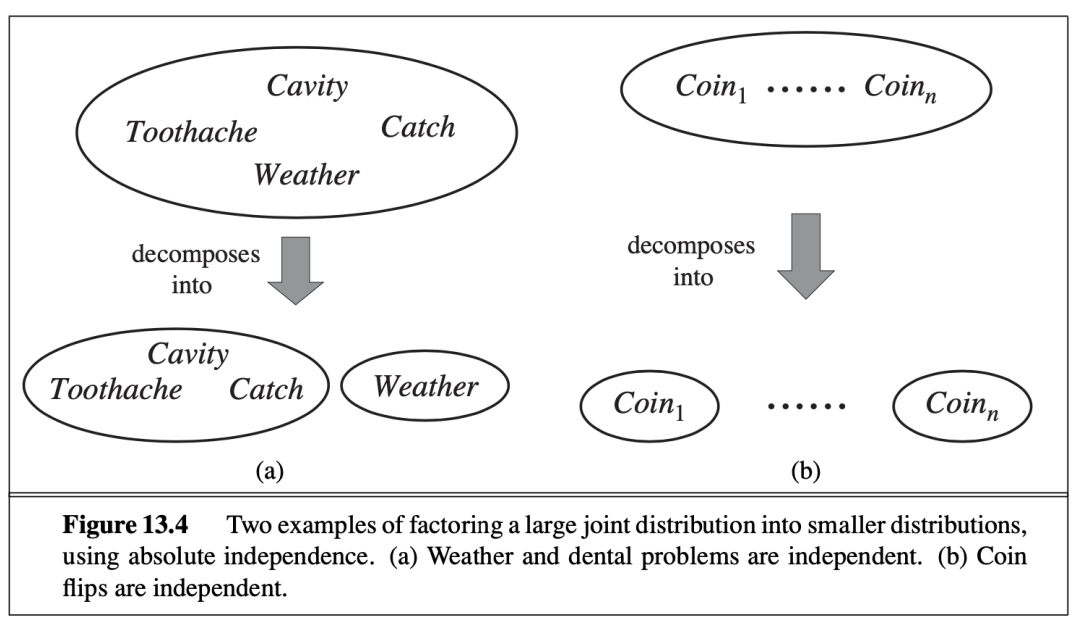
- 四種變數的情況
- 解維度

- 獨立的

- 獨立事件的概念
Bayes’ Rule

- 更廣泛的形式
Applying Bayes’ rule: The simple case

- 可以去推知一個原因對於結果的影響

- 從causal 推得diagnostic
- 腦膜炎與頸部僵硬的例子

- 如果不知道腦膜炎單獨的機率 可以換種形式求解

- 有時換形式會變簡單 有的時候不會

- 診斷有的時候 會導致無條件機率更不穩定
- 比如說腦膜炎突然流行 則發生腦膜炎的無條件機率就會大增加
- 這種情況下 透過計算得出結果(有頸部僵硬的前提 會發生腦膜炎的機率) 而不是統計
- 可以更快速的得到新的結論
- 至於(有腦膜炎的前提 會有頸部僵硬的機率則不會改變) 因為這反映了腦膜炎的行為模式

Using Bayes’ rule: Combining evidence
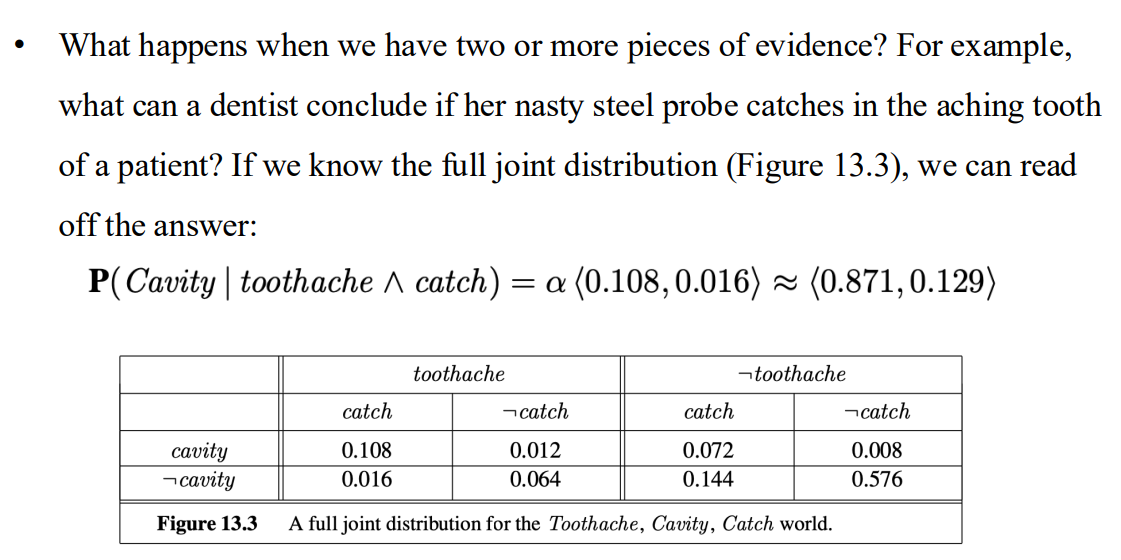
- 先看看答案

- 對於每個evidence variable 我們都需要知道他的條件組合的機率
- 嘗試解釋 讓證據變數是互相獨立的

- 因此可以拆開


- general的長相 表示條件機率的size成長速度會減少


- 這樣的獨立斷言 可以讓我們去擴大整個機率模型的規模
Naïve Bayes Models

- 最終長相
- 雖然獨立斷言 並非絕對獨立 導致天真 但效果往往不錯

Chapter 12 Quantifying Uncertainty
https://z-hwa.github.io/webHome/[object Object]/Introduction to Artificial Intelligence/Chapter-12-Quantifying-Uncertainty/








